Key Concepts
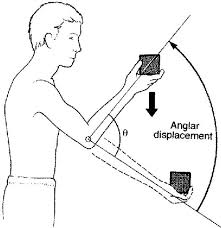
Angular Displacement
Change in angular position of a rotating object.
θ (in radians)
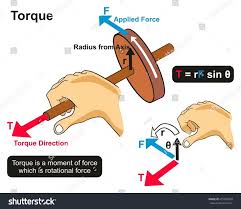
Torque
The rotational equivalent of force.
τ = r × F
Moment of Inertia
Measure of an object's resistance to angular acceleration.
I = Σmr²

